Frações

As frações correspondem a uma representação das partes de um todo. Ela determina a divisão de partes iguais sendo que cada parte é uma fração do inteiro.
Como exemplo podemos pensar numa pizza dividida em 8 partes iguais, sendo que cada fatia corresponde a 1/8 (um oitavo) de seu total. Se eu como 3 fatias, posso dizer que comi 3/8 (três oitavos) da pizza.

Importante lembrar que nas frações, o termo superior é chamado de numerador enquanto o termo inferior é chamado de denominador.

Tipos de Frações
Fração Própria
São frações em que o numerador é menor que o denominador, ou seja, representa um número menor que um inteiro. Ex: 2/7
Fração Imprópria
São frações em que o numerador é maior, ou seja, representa um número maior que o inteiro. Ex: 5/3
Fração Aparente
São frações em que o numerador é múltiplo ao denominador, ou seja, representa um número inteiro escrito em forma de fração. Ex: 6/3= 2
Fração Mista
É constituída por uma parte inteira e uma fracionária representada por números mistos. Ex: 1 2/6. (um inteiro e dois sextos)
Obs: Há outros tipos de frações, são elas: equivalente, irredutível, unitária, egípcia, decimal, composta, contínua, algébrica.
Operações com Frações
Adição
Para somar frações é necessário identificar se os denominadores são iguais ou diferentes. Se forem iguais, basta repetir o denominador e somar os numeradores.
Contudo, se os denominadores são diferentes, antes de somar devemos transformar as frações em frações equivalentes de mesmo denominador.
Neste caso, calculamos o Mínimo Múltiplo Comum (MMC) entre os denominadores das frações que queremos somar, esse valor passa a ser o novo denominador das frações.
Além disso, devemos dividir o MMC encontrado pelo denominador e o resultado multiplicamos pelo numerador de cada fração. Esse valor passa a ser o novo numerador.
Exemplos:
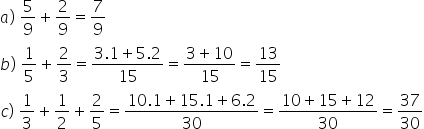
Subtração
Para subtrair frações temos que ter o mesmo cuidado que temos na soma, ou seja, verificar se os denominadores são iguais. Se forem, repetimos o denominador e subtraímos os numeradores.
Se forem diferentes, fazemos os mesmos procedimentos da soma, para obter frações equivalentes de mesmo denominador, aí sim podemos efetuar a subtração.
Exemplos
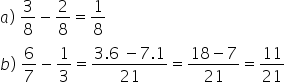
Multiplicação
A multiplicação de frações é feita multiplicando os numeradores entre si, bem como seus denominadores.
Exemplos
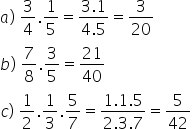
Divisão
Na divisão entre duas frações, multiplica-se a primeira fração pelo inverso da segunda, ou seja, inverte-se o numerador e o denominador da segunda fração.
Exemplos



