Regra de Três, Razão e Proporção: resumo com Simulado Enem

Tudo começa na Regra de Três simples – A regra de três
simples é um método prático para resolver problemas que
envolvem duas grandezas direta ou inversamente
proporcionais. Esta teoria será discutida por meio dos
exercícios a seguir apresentados de Razão e Proporção:

Exemplos de Regra de Três:
Exemplo 01 – Uma máquina varredeira limpa uma área de 5.100 m2 em 3 horas de trabalho. Esta é a
descrição da situação. Agora, vamos à pergunta que temos de resolver: Nas mesmas condições, em quanto
tempo limpará uma área de 11.900 m2?
Vamos ao raciocínio para a resolução: Há aqui duas grandezas: a área e o tempo. Dobrando a área
também se dobra o tempo; triplicando a área também se triplica o tempo, e assim por diante.
Desse modo, são grandezas diretamente proporcionais e, assim, têm o quociente constante. Veja abaixo
como representar com flechas as grandezas para facilitar o raciocínio de Razão e Proporção.
Grandezas Diretamente Proporcionais
Apenas como recurso didático, utilizam-se duas flechas de mesmo sentido para identificar que as grandeza
são diretamente proporcionais. É um fundamento para você praticar bem Razão e Proporção. No exemplo
deste exercício temos duas grandezas ( área e tempo) que são diretamente proporcionais. Veja como utilizar
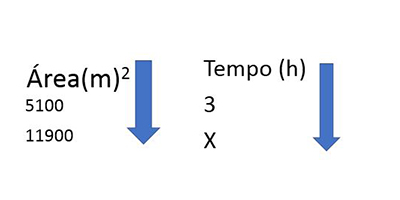
as flechas: Assim, com esta representação que utiliza as flexas para
‘montar o problema’, fica mais fácil também para trabalhar o cérebro e seguir adiante. Veja o próximo passo,e a solução do problema:
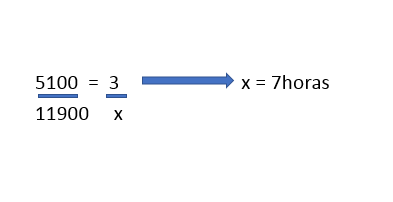
( a grandeza; 11900 foi mutiplicada pelo 3. resultando o valor de 35700, e o 5100 foi multiplicada pelo X, depois o x que estava mutiplicando desce dividindo o 35700, no final, o resultado foi 7. Resumo; a regra de 3 nada mais é que uma mutiplicação cruzada, em x. )
A solução clássica você já sabe: Você faz a multiplicação cruzada, montando (x . 5100) = (3 . 11900). Em
seguida você verfica que 5100.x = 35700 e, ao isolar o x , você
fica com 35700 dividido por 5100 para chegar ao resultado final: xé igual a 7 horas.
Exemplo 02 de Razão e Proporção
Um muro foi construído por 8 operários em 30 dias.
Quantos dias seriam necessários para a construção deste mesmo muro, se fossem utilizados 12
operários?
TEXTO DE APOIO – PROPORÇÃO
Acompanhe a Resolução: Novamente estamos diante de duas grandezas: operários e dias. Mas, aqui, ao
tempo em que uma aumenta (operários) a outra diminui (dias). Pensando em Razão e Proporção, você
poderia escrever que elas têm uma relação inversa neste caso: são grandezas inversamente proporcionais,e por isso as setas invertidas. Veja: Uma maneira de resolver é utilizando o
conceito de grandezas, que são inversamente proporcionais: produto constante. Pode ser assim:
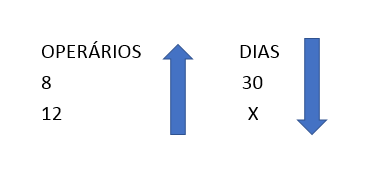
(Nesse caso, não precisa mutiplicar de forma cruzada , basta mutiplicar em linha as grandezas, já que são inversamente proporcional)

Dica de resolução > Outra forma é usar o recurso didático das flechas, como indicado acima. Se são
inversamente proporcionais, as flechas são colocadas em sentido contrário. A seguir criou-se uma proporção,
mantendo-se a fração onde se encontra a incógnita e invertendo-se a outra.
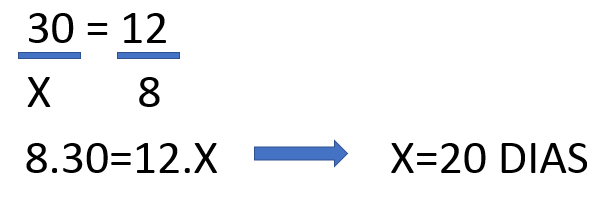
(Nesse caso, uma das grandezas foram invertidas; 12/8, assim mantendo a proporção correta, portanto, nesse sentido, pode resolver a regra de 3, da forma tradicional, basta multiplicar as grandezas de forma cruzada)
Veja também;


Regra de Três Composta
Agora vamos mudar de patamar um pouco, e aprender (ou revisar) Regra de Três Composta. Uma regra de
três é considerada composta quando envolver três ou mais grandezas para que se estabeleçam entre elas a
Razão e a Proporção.
Exemplos para você não esquecer Razão e Proporção
Exemplo 01 – Uma casa é construída por 40 operários trabalhando 9 horas por dia durante 6 dias. Em
quantos dias 24 operários poderiam construir a mesma casa, trabalhando 5 horas por dia?
Resolução: Perceba que ao contrário do exemplo 01 agora nós temos 3 (tres) grandezas para trabalhar:
operários, as horas trabalhadas por dia, e os dias (duração da obra):

Inicia-se colocando uma flecha para baixo na grandeza que possui a incógnita (dias) e a seguir compara-se
com as outras duas. Operários e dias são grandezas inversamente proporcionais e horas por dia e dias também
são inversamente proporcionais. Portanto, as flechas nessas grandezas devem ter sentido contrário:

Para finalizar esse dispositivo prático, iguala-se a fração que contém a incógnita ao produto das demais,respeitando o sentido das flechas:

Exercícios sobre Regra de Três, Razão e Proporção
Exercício 01
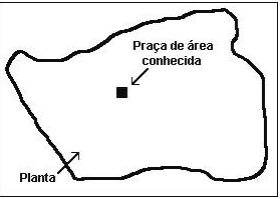
(ENEM, 2001) Um engenheiro, para calcular a área de uma cidade, copiou sua planta numa folha de papel de
boa qualidade, recortou e pesou numa balança de precisão, obtendo 40 g. Em seguida, recortou, do mesmo
desenho, uma praça de dimensões reais 100 m × 100 m, pesou o recorte na mesma balança e obteve 0,08 g.
Com esses dados foi possível dizer que a área da cidade, em metros quadrados, é de, aproximadamente
Exercício 02
(ENEM, 2010) Um dos grandes problemas da poluição dos mananciais (rios, córregos e outros) ocorre pelo
hábito de jogar óleo utilizado em frituras nos encanamentos que estão interligados com o sistema de esgoto.
Se isso ocorrer, cada 10 litros de óleo poderão contaminar 10 milhões (107) de litros de água potável.
Suponha que todas as famílias de uma cidade descartem o óleo das frituras nos encanamentos e consumam
1.000 litros de óleo em frituras por semana. Qual seria, em litros, a quantidade de água potável contaminada
por semana nessa cidade?
Exercício 03
(FCC-SP,) Se 25 operários trabalhando 10 horas por dia abriram um canal com 238 m de comprimento em 17
dias, quantos operários serão necessários para abrir 686 m do mesmo canal em 25 dias de 7 horas de trabalho?
Exercício 04
(UNIMEP) Se dois gatos comem dois ratos em dois minutos, para comer 60 ratos em 30 minutos serão
necessários:
Exercício 05
(UFMG) No ano passado, uma equipe de 13 professores, com um ritmo de trabalho supostamente constante,
corrigiu 3.000 provas em 6 dias. Este ano, o número de provas aumentou para 5.500 e a equipe foi ampliada
para 15 professores. Para se obter uma estimativa do número n de dias necessários para totalizar a correção,
suponha que, durante todo o período de correção, o ritmo de trabalho da equipe deste ano será o mesmo da
equipe do ano passado. O número n satisfaz a condição:
Questão 06
(ENEM cancelado, 2009) Os calendários usados pelos diferentes povos da Terra são muito variados. O
calendário islâmico, por exemplo, é lunar, e nele cada mês tem sincronia com a fase da Lua. O calendário
maia segue o ciclo de Vênus, com cerca de 584 dias, e cada 5 ciclos de Vênus corresponde a 8 anos de 365
dias da Terra.
Quantos ciclos teria, em Vênus, um período terrestre de 48 anos?
Questão 07
(ENEM cancelado, 2009) Pneus usados geralmente são descartados de forma inadequada, favorecendo a
proliferação de insetos e roedores e provocando sérios problemas de saúde pública. Estima-se que, no Brasil,
a cada ano, sejam descartados 20 milhões de pneus usados. Como alternativa para dar uma destinação final a
esses pneus, a Petrobras, em sua unidade de São Mateus do Sul, no Paraná, desenvolveu um processo de
obtenção de combustível a partir da mistura dos pneus com xisto. Esse procedimento permite, a partir de uma
tonelada de pneu, um rendimento de cerca de 530 kg de óleo.
Considerando que uma tonelada corresponde, em média, a cerca de 200 pneus, se todos os pneus
descartados anualmente fossem utilizados no processo de obtenção de combustível pela mistura com xisto,
seriam então produzidas:
Questão 08
(ENEM, 2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos
não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros
10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30
novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da
campanha.
Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao
final do prazo estipulado seria de:
Questão 09
(ENEM, 2011) Muitas medidas podem ser tomadas em nossas casas visando à utilização racional de energia
elétrica. Isso deve ser uma atitude diária de cidadania. Uma delas pode ser a redução do tempo no banho. Um
chuveiro com potência de 4.800 kWh consome 4,8 kW por hora.
Uma pessoa que toma dois banhos diariamente, de 10 minutos cada, consumirá, em sete dias, quantos kW?
Questão 10
(PUCAMP) Sabe-se que 5 máquinas, todas de igual eficiência, são capazes de produzir 500 peças em 5 dias,
se operarem 5 horas por dia. Se 10 máquinas iguais as primeiras operassem 10 horas por dia durante 10 dias,
o número de peças produzidas seria:
Uffa! terminamos, se chegou até aqui, participe do nosso grupo de estudos do facebook.



